《名家专栏》量子技术的发展与应用

量子理论由1900年被普朗克（Max Planck）提出后，爱因斯坦（Albert Einstein）、玻尔（Niels Bohr）、海森堡（Werner Heisenberg）、薛定谔（Erwin Schrödinger）等人不断提出新理论并涌现出相关实验。这些物理先驱所做的开创性工作和思维变革，颠覆了经典力学对自然界的认知，从而引发对微观粒子运动更精确和深入的研究，形成了量子力学这一套系统而严谨的学科。量子力学与对应的技术在整个20世纪飞速地发展，许许多多的科技成果与新物态发现都与量子技术息息相关，其在生活、军事、科研等领域的应用也层出不穷。随着量子技术的高速发展，其衍生出的不同应用领域，如量子通信、量子计算以及量子测量等领域不断出现新的突破。其中，例如量子计算机、原子钟等应用都在各自的领域打破了经典技术的极限，成为了前沿科技发展必不可少的技术。 

正文

量子力学是由许多现代物理学家共同创立的新物理学科，是研究物质世界微观粒子运动规律的物理学理论，主要研究原子、分子、凝聚态物质以及原子核和基本粒子的结构、性质。区别于经典力学、相对论，量子力学从根本上改变了人们对物质结构以及相互作用的理解，明确解释了原子世界“微观宇宙”的奇异属性。这些基于物质微观世界的理论催生出了量子革命，改变了世界面貌。原子弹、芯片、激光等重大发明均是来源于量子力学。量子技术作为基于量子力学发展起来的前沿技术，成为当今尖端科技中的一大热门，发展了一系列颠覆传统方法的新兴技术。

一、量子通信

量子通信是基于量子物理的量子信息学的应用之一，因其原理上具有不可破译特点而受到了学者们的广泛关注。1993年美国IBM公司的研究人员首次设计了利用经典信道和量子信道(Einstein-Podolsky-Rosen, EPR纠缠态)来远距离传输未知量子态的协议，后来被称为量子隐形传态(Quantum teleportation, QT)。1997年奥地利Anton Zeilinger小组利用独立光子偏振态首次实现了QT实验验证。2022年Alain Aspect、John Clauser和Anton Zeilinger因他们在纠缠光子实验、验证违反贝尔不等式和开创量子信息科学方面所做出的贡献而被授予诺贝尔物理学奖。他们各自利用纠缠量子态开展了创新性实验，其研究结果为目前量子信息的新技术奠定了基础。

量子通信泛指通过移动量子态实现信号、信息或量子态的传输和转移的量子技术。近年来，量子通信在理论和实验上取得了重要进展，其中量子密钥分发（QKD）是*先走向实用化和产业化的量子信息技术，它能基于基本物理原理实现合法用户间无条件安全的密钥分发，是应对量子计算对传统加密体系威胁的有效手段。

量子密钥分发是指利用量子态来加载信息，通过一定的协议在遥远地点的通信双方共享密钥。量子力学基本原理保证了密钥的不可窃，从而在原理上实现无条件安全的量子保密通信。为实现绝对安全的保密通信，Benett与Brassard于1984年提出了首个量子密钥分发协议，即著名的BB84协议[1]。该协议运用不确定性原理实现非正交状态量子信息的编码，利用光子的偏振态对密钥进行编码。这种方案的安全性基于量子力学的两个基本原理：单光子的不可分割性和单光子量子态的测量塌缩性。

目前，QKD的发展重心已转移至实用化方向。2003年由美国国防部高级研究计划局资助的Havard大学、Boston大学和BBN科技合作建立了世界上首个量子通信网络，后扩展为10节点量子通信网络。2004年欧洲在维也纳启动建设基于量子加密的安全通信网络，并于2008年建立了6节点多协议类型的8条链路的量子通信网络。2010年日本在东京建立了城际高速量子保密通信网络，并进行了一次一密的安全时频会议应用演示。

在国内，2012年国家量子通信骨干网络计划即量子京沪干线在国内率先启动QKD技术的应用，其于2017年9月正式全线开通。2017年中国科学技术大学潘建伟院士团队利用“墨子号”量子科学实验卫星在国际上率先成功实现了千公里级的星地双向量子纠缠分发。此外，他们利用墨子号还实现了北京到维也纳的洲际量子密钥分发。

图 1天地一体化量子网络[2]

2021年中国科大潘建伟院士团队在量子保密通信京沪干线与“墨子号”量子卫星成功对接的基础上，构建了世界上首个集成700多条地面光纤QKD链路和两个星地自由空间高速QKD链路的广域量子通信网络，实现了地面跨度4600公里的星地一体的大范围、多用户量子密钥分发[2]。

2024年中国科学技术大学潘建伟院士团队实现了全天候的自由空间QKD[3]。他们使用625 MHz诱骗态光源和傅里叶极限白天噪声抑制技术，在20 km自由空间获得了495 bps密钥成码率的结果。通过地基实验在信道损耗和噪声水平方面有效验证了未来构建基于量子星座的星地、星间量子通信网络的可行性，为更长的过境时间、更多的密钥分发量和万公里量级的量子纠缠分发提供基础。

二、量子计算

量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式。与经典计算不同，量子计算遵循量子力学规律，它是能突破经典算力瓶颈的新型计算模式。量子计算机，作为执行量子计算任务的设备，以量子比特（qubit）为基本运算单元。在量子计算中，基于量子叠加原理，量子比特的不同状态可被同时存储和处理。

量子力学的基本特性是叠加态，该原理使得量子信息单元的状态可以处于多种可能性的叠加状态，从而导致量子计算从效率上相比于经典计算具有更大潜力。普通计算机中的2位寄存器在某一时间仅能存储4个二进制数（00、01、10、11）中的一个，而量子计算机中的2位量子位寄存器可同时存储这四种状态的叠加状态。随着量子比特数目的增加，对于n个量子比特而言，量子信息可以处于2n种可能状态的叠加，配合量子力学演化的并行性，可以展现比传统计算机更快的处理速度。

量子计算的概念在80年代初期提出，并经由1985年图灵机的概念具备了数学基本型式。而自从1994年贝尔实验室的P. Shor证明了量子算法的实用性[4]，越来越多的量子算法被提出。许多量子系统也可作为量子计算的基础架构，例如光子偏振、腔量子电动力学和离子阱等。基于量子计算的量子计算机将大大超过传统计算机，各国也都在致力于发展性能更好和量子位更多的量子计算平台。

加拿大量子计算公司D-Wave于2011年正式发布全球第一款商用型量子计算机D-Wave，开启量子计算机的热潮。并在2017年推出D-Wave 2000Q，超越经典的专业算法1000-10000倍。而与此同时算法也在不断的更替，从早期的Shor和Grover算法，逐渐发展到寻找*优解，收敛速度更快的HHL、QAOA和F-VQE等算法[5]。

近年来，量子计算产业链和应用以各互联网企业为核心进行发展。国外方面，IBM、谷歌、微软、霍尼韦尔和亚马逊等互联网企业均在量子计算领域有所布局，开展了量子计算的全面研发，包括硬件、算法以及软件等。IBM基于超导路线已研发127量子比特处理器“Eagle”，推出开源Qiskit Metal量子软件；谷歌研制成功53量子比特计算机“悬铃木”，拥有TensorFlow-Quantum和FermiNet等多款应用软件。此外，D-Wave、IonQ和Regetti Computing等企业也在积极投入量子计算研发。并且量子技术已上升至国家技术层面，如美国国防部（DAPRA）和欧盟都制定了国家级别的量子技术战略目标布局计划，俄罗斯和日本也在陆续启动多项规划。

国内在量子计算方面也取得了全球瞩目的成就。2021年中科院潘建伟团队通过超导路线对量子比特进行调控，先后研制成功62位可编程超导量子计算机原型“祖冲之号”，如图 2左图所示；以及66位“祖冲之二号”；经评估，其采样复杂程度超越谷歌“悬铃木”2-3个数量级。而利用室温下即可实现的光量子路线，中科大研究团队于2020年成功构建76个光子的“九章”量子计算原型机，如图 2右图所示，并在次年突破至113个光子，比超级计算机速度快1024倍。2018年，华为公布了量子计算模拟器HiQ云服务平台；2020年百度也推出了百度量子平台，并在2022年发布了产业级超导量子计算机“乾始”。量子计算以其远超传统计算机的速度，将在数字信号处理、军事智能、物流管理等需要强大计算能力的领域大展宏图。

图 2 “祖冲之号”量子处理器（左）“九章”光量子干涉实物图（右）图源：维基百科

三、量子模拟

1982年，在费曼的一次演讲"Simulating physics with computers"中[6]，首次明确提出了量子模拟的概念。他指出，由于在量子力学系统中基的空间随粒子数目呈指数增长，经典计算机很难解决此类问题。一种可行的解决方法是"A quantum for a quantum"，即通过量子系统来“模拟”量子系统。这也就是量子模拟的基本思想。量子模拟器会通过构造与目标体系等效的哈密顿量来模拟对应的系统，给出定量或定性的结论。

冷原子是一类非常重要的量子模拟体系，由于其易于操控和测量的特点，可用于多种物理体系的构建。冷却至低温的玻色子与费米子展现出了良好的量子简并性，在Feshbach共振下，可对原子间的散射长度进行较为自由的调节，这对于研究多体与少体相互作用的物理机制有着重要的意义。

关于Feshbach共振对量子系统的调控，Yoshiro Takahashi等人成功实现了亚微米空间尺度的Feshbach共振调控，并利用衍射图样拟合了散射长度的大小[7]。散射长度的空间调制证明了原子相互作用的高分辨率控制是可能的，该灵活性也说明了可以利用量子系统进行模拟。

Gustavsson等人展开了玻色-爱因斯坦凝聚态（BEC）原子的Bloch振荡的研究[8]，他们利用Feshbach共振将原子间相互作用调至0，在这样的条件下观察到了超过2万次的Bloch振荡，能够在无相互作用的极限下实现基于BEC的原子干涉仪。

国内关于Feshbach共振的研究也有许多，例如张婧、李东豪教授小组在实验上成功实现了p波Feshbach共振技术，利用激光实现束缚态的跃迁[9]，如图 3所示。而在聂亮、张越等人的工作中，成功实现了同核和异核Feshbach共振，为模拟量子流体等相互作用提供了理想的平台[10]。

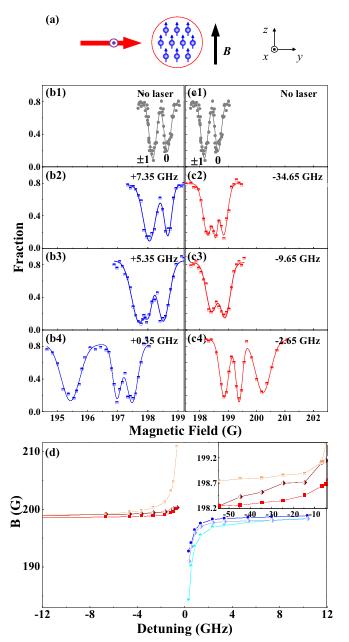
图 3 由光场驱动的p波Feshbach共振[10]

光晶格则使得冷原子量子模拟的对象大大增加，通过构造周期性势场，可以对多种格点体系进行模拟，如图 4所示[11]。晶格中这种超冷原子的相互作用由Hubbard模型给出。Hubbard模型是一种基本的量子模型，可对磁性和超流等现象有所解释。目前的冷原子实验已能够实现低温下Hubbard模型中的多种相变。此外，目前人们也正在尝试在冷原子系统中构建人造规范势，从而模拟具有规范荷（如电荷）的体系，通过这种方法揭示量子霍尔效应、拓扑绝缘体等现象的内在机制。

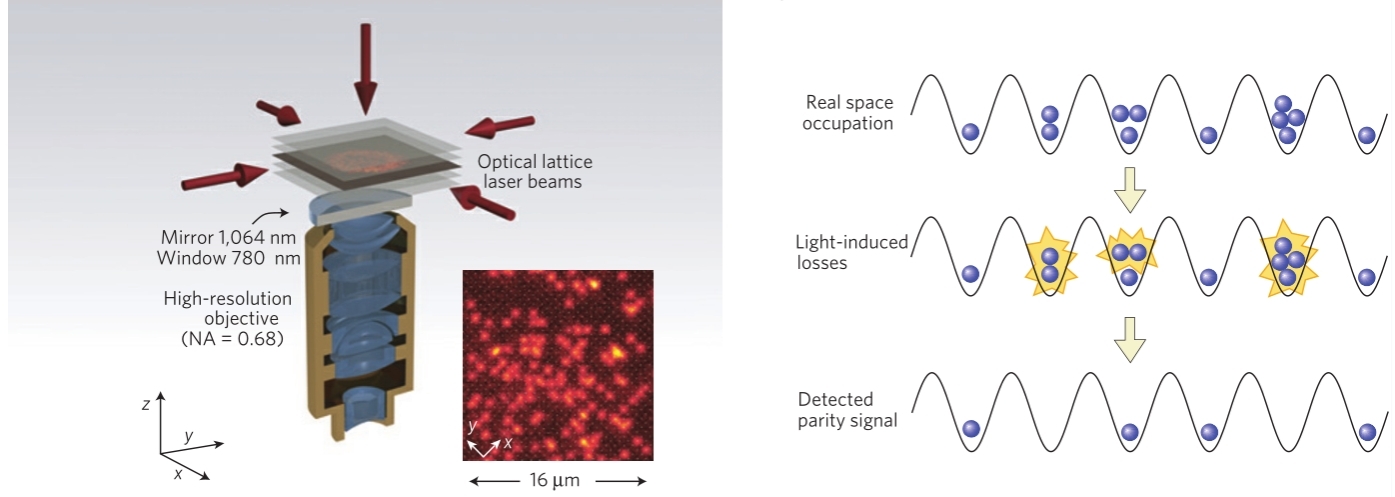
图 4 光晶格中的超冷原子[11]

Immanuel Bloch等人研究了光晶格中冷原子的相变[12]。由Hubbard模型给出，相邻格点的跳变由隧道耦合能和各点相互作用能表征，对于排斥性的玻色子，利用晶格深度的增加，相互作用达到某一临界强度时，系统会经历由超流体转变为Mott绝缘态的相变。

而光学晶格量子模拟中*活跃的问题之一就是Fermi-Hubbard模型的实现[13]，可为材料的电子和磁性提供重要依据。而将费米量子气体加载进光晶格中的实现，让Fermi-Hubbard模型成为可能。这样的Fermi-Hubbard模型中，哈密顿量由干涉激光场和超冷原子碰撞产生，给予途径模拟哈密顿量，并能够解决许多多体系统的开放问题。

而除了光晶格系统中的Hubbard模型，还存在其它模型，例如伊辛模型。伊辛模型是描述物质铁磁相变的重要模型，而量子系统在模拟一维和二维伊辛模型上均有重要进展。2023年，IBM团队利用127比特的量子系统实现了对超过100个自旋的二维横向伊辛场模型的动力场模拟，超越了经典近似方法模拟的计算精度，之后可进一步走向实用化。

量子模拟还可以解决拓扑物理系统和其他多体问题。拓扑物理是凝聚态物理研究的重要方向之一，理解物质的拓扑性质有助于研究更为稳定的拓扑量子计算机。目前，超导量子计算机已经可以模拟各类物理模型中的拓扑物理性质：比如一维超导模型Kitaev链的拓扑相变的模拟；利用变分能量求解算法，实现对二维超导体波函数拓扑不变量，包括陈数，几何相变的模拟；模拟二维陈绝缘体能带、拓扑零能模和拓扑非平庸边缘态等。此外，在模拟流体力学系统、天体物理与高能物理系统等方面均是量子模拟可应用的方向。近年来，基于超冷原子的量子模拟取得了巨大的进展，彻底改变了我们探测微观系统的方式，通过精密的原子操控，能够实现对多体系统的高还原度模拟，为各领域的理论预言和实验验证提供有效的手段。

四、量子测量

量子测量是量子力学*基本和核心的问题之一。经典物理中的测量过程为对被测者不加改变的提取，然而在量子体系中，根据冯·诺依曼的测量假定，量子测量会导致量子态塌缩至待测物理量的本征态，即不同于经典测量，量子测量会对被测系统产生影响，相同的量子系统被测量后可能会获得完全不同的结果，而这些结果将符合一定的概率分布。

量子测量基于微观粒子量子态精密测量，完成被测系统物理量的执行变换和信息输出，在测量精度、灵敏度和稳定性等方面与传统测量技术相比有明显优势。在量子测量方面，目前已经研发并攻克了多项技术，例如原子的激光冷却与俘获技术、原子喷泉技术和物质波干涉操控技术等关键技术。通过这些技术而实现的量子测量，可以了解量子的物理状态和原子微观性质，从而更好地对其进行应用。原子干涉仪，原子陀螺仪，原子钟等均是量子测量领域代表性成果。

4.1 原子干涉仪

1924年德布罗意首次提出了粒子的波动特性，粒子的波长由粒子的动量决定，物质波是量子力学理论的基本概念之一。物质波干涉技术在此理论基础上发展起来，随着对原子结构及其物理性质的理解，利用原子干涉技术进行引力测量的实验也逐步被实现。

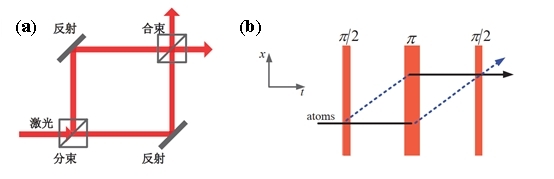
图 5 (a)Mach-Zehnder光学干涉仪示意图 (b)三脉冲原子干涉仪示意图

Mach-Zehnder光学干涉仪原理图如图 5(a)所示，从光源发出激光经分束镜后分成两束，两束激光经过不同的路径分别被不同反射镜反射，再一次经过分束镜时发生干涉，*后通过探测器读出干涉信号后可得到相关相位信息。在光学干涉仪中，激光携带被测量的相位信息，而分束器和反射镜改变光的路径，激光的动量在被物质吸收和再反射时发生变化。原子干涉仪的工作原理与Mach-Zehnder光学干涉仪类似，而原子干涉仪将原子作为物质波，光脉冲作为光学元件，获得的相位差包含原子经历外场的所有信息，如重力加速度、重力梯度、地球转动和磁场等。

目前各种各样的原子干涉实验正利用原子的波动特性进行精密测量和量子力学基本原理的检验。原子干涉仪具有较高的灵敏度和很好的长期稳定性，比较常用的原子干涉仪可分为原子干涉重力仪、原子干涉梯度仪和原子干涉陀螺仪等。可用于重力加速度测量、重力梯度测量和引力场曲率测量、万有引力常数测量、地球转动测量、精细结构常数测量、微观距离下的引力研究以及暗物质探测等。还可比较不同重力原子的自由下落以及不同自旋方向、不同超精细能态的原子来检验广义相对论中的弱等效原理。此外，还可在空间中用原子干涉仪探测引力波。目前，利用原子干涉仪进行高精度重力测量的实验以达到了4.2 μGal rad/s/Hz1/2的短期灵敏度[14]，利用原子干涉仪进行弱等效原理检验的实验已经达到了10-12的较高水平[15]。

4.2 原子陀螺

陀螺仪可提供全自主、实时、连续的导航技术，成为实现高精度无缝导航的关键技术。惯性导航陀螺仪可分为光学陀螺仪、微机电陀螺仪与原子陀螺仪等。

利用碱金属原子的进动测量磁场大小可实现磁力计，提高原子磁力计的灵敏度可研制高性能的原子陀螺仪。原子陀螺仪根据工作原理不同可分为原子自旋式陀螺仪以及原子干涉式陀螺仪等，其中原子自旋式陀螺仪包括无自旋交换弛豫(Spin exchange relaxation free, SERF)陀螺仪、核磁共振(Nuclear magnetic resonance gyroscope, NMRG)陀螺仪等。陀螺仪中的角度随机游走(Angle random walk, ARW)和漂移稳定性(Bias stability)是表征其性能的两个主要指标。相较于光学陀螺仪和微机电陀螺仪，原子陀螺仪具有精度高、体积小且对加速度不敏感的优点。

4.2.1 无自旋交换弛豫陀螺仪

SERF原子自旋陀螺仪利用电子自旋敏感物体转动，具有精度高、体积小的特点。其主要工作过程为原子SERF态制备以及原子自旋进动检测。其工作原理如图 6所示，磁屏蔽装置使原子处于近零磁场环境中，此时碱金属原子的拉莫尔进动频率大幅降低，同时由于高密度高压环境使自旋交换率极大提升，从而充分抑制原子的自旋交换弛豫，实现SERF态。当载体转动时，由于电子自旋的定轴性，检测激光与电子自旋产生的宏观磁矩M间存在夹角α，通过检测该角度即可得到载体转动信息。

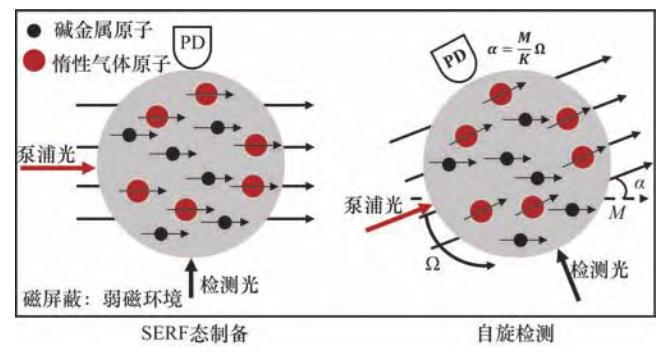
图 6 无自旋交换弛豫陀螺工作原理[16]

21世纪初普林斯顿大学Romalis首次实现了基于SERF效应的超高灵敏度原子磁强计[17]，2018年普林斯顿Romalis团队和Twinleaf公司使用87Rb磁强计抑制Rb原子之间的自旋交换弛豫，在直径10 mm的气室下，实现了角度随机游走0.025°/h1/2，零偏稳定性优于0.01°/h的SERF陀螺仪。北京航空航天大学房建成院士团队在2008年率先开展基于原子自旋的超高灵敏度磁场测量与惯性测量技术研究，在2018年研制了零偏稳定性优于0.05 °/h的双轴SERF陀螺，在2019年研制出小型化SERF陀螺原理样机，在2020年陀螺仪原理样机的零偏稳定性达到0.001 °/h量级[18]。

4.2.2核磁共振陀螺仪

NMRG陀螺仪利用磁场中原子核自旋的进动即拉莫尔进动来测量旋转[19]，兼顾低功耗、体积小、低成本、高精度和抗振动等综合优势，目前发展较为成熟。在核磁共振陀螺中，原子核自旋可以在惯性空间中保持其原始指向，所以可以用原子核自旋对转动的敏感研制核磁共振陀螺仪，其装置原理图如图 7所示。

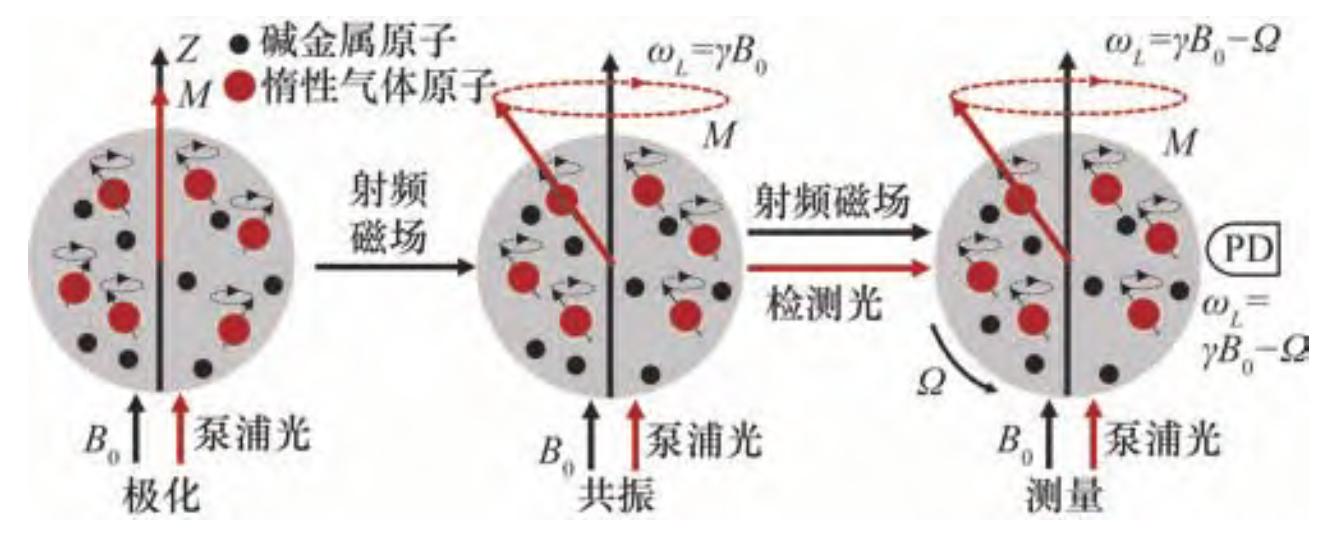
图 7 核磁共振陀螺仪原理示意图[16]

原子核自旋具有磁矩μ，取向与自旋轴方向一致，在自然状态下具有随机性，无宏观指向，将核自旋置于静磁场B0中，核自旋将在静磁场作用下以拉莫尔角频率绕?0方向进动。在此基础上，作用与磁场B0方向相同的泵浦光后，可使得原子被极化，赋予核自旋宏观指向。通过在正交于已有稳定静磁场B0方向外加频率与原子进动频率相等均匀的交变电磁场B1(t)，核自旋会产生核磁共振，且共振频率等于拉莫尔角频率。探测光与载体固定并且随其共同旋转，探测光检测宏观核自旋的拉莫尔进动频率，能够获得载体旋转的角速度，也可计算求解静磁场B0的大小

4.2.3 原子干涉陀螺仪

原子干涉陀螺仪的原理与光学干涉陀螺仪类似，利用了原子作为物质波的波动性，基于Sagnac效应完成角速度的测量。原子干涉陀螺仪工作过程主要包含原子团制备、原子分束、原子反射、原子合束和干涉相位测量，其基本原理如图 8所示。原子束中的原子经内态选择后全部处于基态，然后经拉曼光脉冲分别实现分束、反射和合束，*后通过干涉条纹的相位测量获取转动信息。

图 8受激拉曼跃迁和原子干涉陀螺原理图

随着激光冷却原子技术的发展，第一个脉冲型冷原子干涉陀螺仪于2003年由法国巴黎天文台Landragin小组实现[22]。2018年，该小组实现了首个零偏不稳定性低于1nrad/s的原子干涉陀螺仪，其短期灵敏度为3×10-8 rad/s/Hz1/2，零偏不稳定性为3.0×10-10 rad/s@4000s[23]。2022年中国科学院精密测量科学与技术创新研究院采用冷原子双平抛方案，灵敏度为1.5×10-7 rad/s/Hz1/2，零偏不稳定性为9.5×10-9 rad/s@20000s[24]。近年来，原子干涉陀螺仪逐渐从实验室环境走向工程应用，这一过程中还有许多问题亟待解决。其中，既有保持精度前提下的集成化、小型化和提高系统鲁棒性与自动化程度的工程技术问题，也有提高数据更新率、带宽和动态范围的基础技术问题，后者是制约目前原子干涉陀螺仪动态环境应用的瓶颈技术问题。

4.3 原子钟

时间是描述事件发生前后序列的物理量。随着精密计时工具的发明，天文秒不是恒定不变的。量子力学的建立和发展使科学家认识到原子内部电子能级间的特征跃迁频率具有比天文现象更高的稳定度，不随时间和地点的变化而变化，更适用于作为时间标准，从而产生了原子钟。由原子钟生成的秒，称为“原子秒”。

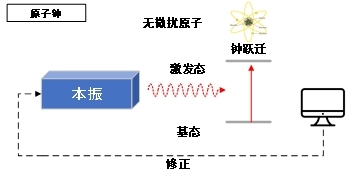
图 9 原子钟基本原理示意图

原子钟的工作原理如图 9所示，使用本振源(晶振或者超稳频率源)的标准频率。一路作为输出，另一路通过频率综合器得到特定频率数值输出原子钟跃迁频率。将此频率信号作用于原子系综，使原子发生能级跃迁，利用跃迁几率作为误差信号反馈至本振源，*终将本振源的频率锁定到原子跃迁频率上。

1955年，英国国家物理实验室研制成国际上第一台铯原子钟[25]。1967年第13届国际计量大会将秒定义在铯133原子在无外界干扰的条件下基态两个超精细能级间跃迁对应的辐射频率上。2018年国际计量大会基于常数的新理念重新表述了秒定义：当铯133原子基态的超精细能级跃迁频率以单位Hz表示时，将其固定数值取为9 192 631 770来定义秒[26]。

光学原子钟(光钟)则是利用频率在光学波段的原子(分子、离子)跃迁作为量子参考而建立的原子钟。根据对量子参考跃迁对象的不同，光钟可分为离子光钟、光晶格钟和核光钟等。离子光钟采用了离子阱技术，利用磁场、静电场或射频场将带电离子囚禁在超高真空中，离子与外界环境较好地隔离，具有系统频移不确定度低的优点，目前世界上*好的离子光钟的系统频移不确定度已进入10-19量级，但是由于目前的离子光钟只囚禁了一个离子，因此受到量子投影噪声限制，使得频率稳定度差于囚禁多个参考粒子的中性原子光钟。中性原子光晶格钟利用光晶格囚禁大量中性原子作为量子参考，通过光晶格把原子囚禁在Lamb-Dicke区域，消除运动效应（热运动和光子反冲）造成的影响，同时引入“魔术波长”光晶格技术，减小由于光晶格激光的引入而造成的系统频移，增加原子与钟跃迁探测激光的作用时间，减小探测的傅里叶极限线宽，实现了1秒平均频率稳定度进入10-17量级。

图 10 光学原子钟实物 图源：JILA

全世界范围内多家单位都在不断提高和突破相关技术以实现更高精度的光钟，国内外主要有171Yb镱光晶格钟、87Sr锶光晶格钟和离子光钟等。在中性原子光晶格钟方面，美国实验室天体物理联合研究所(Joint Institute for Laboratory Astrophysics, JILA)叶军教授小组在2022年实现了在单个真空腔内利用87Sr锶原子分辨微米量级重力红移[27]，有力地证明了光钟在频率计量上的超高分辨特性；他们在2024年首次将光晶格中的原子制备在Wannier-Stark本征态上，获得创记录的相干时间；并精密控制碰撞频移、晶格光频移，以及使用对磁场*不敏感的钟跃迁，评估87Sr锶光晶格钟不确定度为8.1×10-19，正式将光晶格钟的不确定度推进10-19量级[28]。美国国家标准与技术研究所(National Institute of Standards and Technology, NIST) A. D. Ludlow小组在2018年报道了使用辐射屏蔽腔降低Zeeman频移和黑体辐射频移不确定度，评估171Yb镱原子光钟不确定度为1.4×10-18[29]。在离子光钟的不稳定度和不确定度报道方面，NIST的D. R. Leibrandt小组在2019年报道了27Al+铝离子量子逻辑光钟，他们使用新研制的离子阱抑制27Al+铝离子热运动，测得27Al+铝离子光钟的不稳定度和不确定度分别为1.2×10-15/√?和9.4×10-19[30]。中国科学院精密测量科学与技术创新研究院(Innovation Academy for Precision Measurement Science and Technology, APM)高克林教授小组在2022年报道了液氮制冷下不确定度为3×10-18[31]的40Ca+钙离子光钟。除了光晶格钟和单离子钟等光钟外，也有不少研究单位研制出分子光钟[32]、高价离子钟[33]和核光钟[34]等。

结论

量子力学的提出是一里程碑式的人类认知的突破，往后几乎所有伟大的科学发现都和量子技术密不可分。而随着量子技术在量子通信、量子计算、量子测量等领域的不断发展，量子技术的进一步突破已引起人们越来越多的关注。近年来，量子技术领域方兴未艾，其催生的技术变革以及应用发展正在改变世界面貌，成为了诸多前沿领域发展的基石。由于这些技术影响到社会、军事、科技、经济等多方面，各国也都将量子技术的发展定为重大战略目标。量子技术持续不断的突破让科学发展生机勃勃，其发展前景和对未来技术的影响将不可限量，并必将引领新一轮科技革命和产业变革。

作者简介

第一作者：金涛韫、彭成权

通讯作者：徐信业 教授

作者单位：华东师范大学精密光谱科学与技术国家重点实验室

引用文献

1. Bennett, C.H. and G. Brassard. Quantum cryptography: Public key distribution and coin tossing. in IEEE International Conference on Computers, Systems and Signal Processing. 1984.

2. Chen, Y.-A., et al., An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature, 2021. 589(7841): p. 214-219.

3. Cai, W.-Q., et al., Free-space quantum key distribution during daylight and at night. Optica, 2024. 11(5): p. 647-652.

4. Shor, P.W. Algorithms for quantum computation: discrete logarithms and factoring. in Proceedings 35th Annual Symposium on Foundations of Computer Science. 1994.

5. Amaro, D., et al., A case study of variational quantum algorithms for a job shop scheduling problem. EPJ Quantum Technology, 2022. 9(1): p. 5.

6. Feynman, R.P., Simulating physics with computers, in Feynman and computation. 2018, CRC Press. p. 133-153.

7. Yamazaki, R., et al., Submicron spatial modulation of an interatomic interaction in a Bose-Einstein condensate. Physical Review Letters, 2010. 105(5): p. 050405.

8. Gustavsson, M., et al., Control of Interaction-Induced Dephasing of Bloch Oscillations. Physical Review Letters, 2008. 100(8): p. 080404.

9. Peng, P., et al., Universal feature in optical control of a p-wave Feshbach resonance. Physical Review A, 2018. 97(1): p. 012702.

10. 聂亮, et al., ~(39)K-~(87)Rb双组分|F=1,m_F=-1>态玻色-爱因斯坦凝聚体的实验制备. 量子光学学报, 2022. 28(03): p. 215-222.

11. Bloch, I., J. Dalibard, and S. Nascimbene, Quantum simulations with ultracold quantum gases. Nature Physics, 2012. 8(4): p. 267-276.

12. Greiner, M., et al., Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature, 2002. 415(6867): p. 39-44.

13. Esslinger, T., Fermi-Hubbard physics with atoms in an optical lattice. Annu. Rev. Condens. Matter Phys., 2010. 1(1): p. 129-152.

14. Hu, Z.-K., et al., Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter. Physical Review A, 2013. 88(4): p. 043610.

15. Asenbaum, P., et al., Atom-interferometric test of the equivalence principle at the 10− 12 level. Physical Review Letters, 2020. 125(19): p. 191101.

16. 骆曼箬, et al., 原子陀螺研究进展及展望. 测控技术, 2023. 42(10): p. 1-10.

17. Allred, J., et al., High-sensitivity atomic magnetometer unaffected by spin-exchange relaxation. Physical review letters, 2002. 89(13): p. 130801.

18. Fu, Y., et al., Effects of probe laser intensity on co-magnetometer operated in spin-exchange relaxation-free regime. IEEE Transactions on Instrumentation and Measurement, 2022. 71: p. 9501607.

19. Donley, E.A. Nuclear magnetic resonance gyroscopes. in SENSORS, 2010 IEEE. 2010. IEEE.

20. Leete, B.D., Apparatus for measuring angular motion. 1955, Google Patents.

21. Karwacki, F., Nuclear magnetic resonance gyro development. Navigation, 1980. 27(1): p. 72-78.

22. Yver-Leduc, F., et al., Reaching the quantum noise limit in a high-sensitivity cold-atom inertial sensor. Journal of Optics B: Quantum and Semiclassical Optics, 2003. 5(2): p. S136.

23. Savoie, D., et al., Interleaved atom interferometry for high-sensitivity inertial measurements. Science advances, 2018. 4(12): p. eaau7948.

24. Yao, Z.-W., et al., Self-alignment of a large-area dual-atom-interferometer gyroscope using parameter-decoupled phase-seeking calibrations. Physical Review A, 2021. 103(2): p. 023319.

25. Essen, L. and J.V. Parry, An atomic standard of frequency and time interval: a caesium resonator. Nature, 1955. 176(4476): p. 280-282.

26. Milton, M., On the revision of the International System of Units (SI). Draft Resolution A, 2018.

27. Bothwell, T., et al., Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature, 2022. 602(7897): p. 420-424.

28. Aeppli, A., et al., A clock with 8×10-19 systematic uncertainty. arXiv preprint arXiv:2403.10664, 2024.

29. McGrew, W., et al., Atomic clock performance enabling geodesy below the centimetre level. Nature, 2018. 564(7734): p. 87-90.

30. Brewer, S.M., et al., 27Al+ quantum-logic clock with a systematic uncertainty below 10-18. Physical Review Letters, 2019. 123(3): p. 033201.

31. Huang, Y., et al., Liquid-nitrogen-cooled Ca+ optical clock with systematic uncertainty of 3×10-18. Physical Review Applied, 2022. 17(3): p. 034041.

32. Leung, K., et al., Terahertz vibrational molecular clock with systematic uncertainty at the 10-14 level. Physical Review X, 2023. 13(1): p. 011047.

33. King, S.A., et al., An optical atomic clock based on a highly charged ion. Nature, 2022. 611(7934): p. 43-47.

34. Peik, E., et al., Nuclear clocks for testing fundamental physics. Quantum Science and Technology, 2021. 6(3): p. 034002.

免责说明

北京卓立汉光仪器有限公司公众号所发布内容（含图片）来源于原作者提供或原文授权转载。文 章版权、数据及所述观点归原作者原出处所有，北京卓立汉光仪器有限公司发布及转载目的在于传递 更多信息及用于网络分享。

如果您认为本文存在侵权之处，请与我们联系，会第一时间及时处理。我们力求数据严谨准确， 如有任何疑问，敬请读者不吝赐教。我们也热忱欢迎您投稿并发表您的观点和见解。