光学斩波器相位抖动特性分析

摘要：

光学斩波器用于向光源引入稳定的调制。该调制的稳定性可以通过抖动来表征，既斩波波形的边沿时序相对于理想时钟的变化。抖动可以以时间（秒）或相位（度）为单位表示，因此有时称为“周期抖动”或“相位抖动”。在本技术说明中，我们定义了光学斩波实验背景下的抖动，并提供了使用该定义的测量协议和结果。

引言：

顾名思义，光学斩波器用于将连续波光源转换为用户定义频率的斩波波形。斩波周期的变化称为抖动。通常，斩波周期的高度可重复性至关重要，因此抖动是光学斩波器的关键品质因数。因此，了解如何测量抖动对于比较光斩波器产品至关重要。

  通过直观的例子来理解抖动是最容易的。考虑将光学斩波器锁定到稳定的外部参考频率[1]，并将外部参考和斩波的光学信号馈送到示波器。将示波器配置为在稳定参考的边沿触发，通过显示具有持久性的波形，可以很容易地看到抖动如何影响斩波信号：光信号的抖动将导致其边沿模糊，如图1所示。

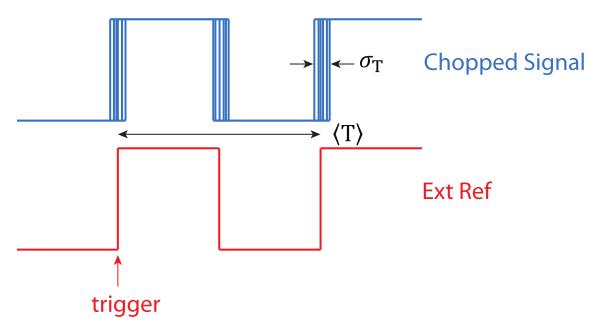
图 1：使用示波器可看到抖动。斩波信号边沿将“抹掉”以周期抖动 σT 为特征的时序分布。通过理想或平均周期 ⟨T ⟩ 标准化，可以将其转换为相位（单位：°）。

如果测量 N 个周期，抖动表示各个测量值 Ti 相对于其平均值 ⟨T ⟩的分布，以峰峰值或 RMS（均方根）表示：

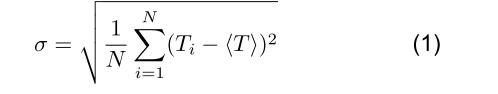
平均抖动可以用秒或度来表示：

抖动特征的时间尺度是多少；即应该收集多少个周期？一般来说，我们选择的时间尺度足够长，以便达到抖动的稳定值，但又不能太长，以免斩波器内部计时的长期频率漂移变得明显。在实践中，这通常相当于几十秒到几分钟的数据收集时间尺度，这取决于斩波频率（N在几百到几万的量级上）。

机械相位还是光学相位？

由于光学斩波器依赖于机械旋转叶片，每次机械旋转都会产生多个光学周期，因此已发布的斩波器规范中关于抖动单位的规定存在一些含糊之处：我们是在讨论机械相位还是光学相位？

  具有 n 个槽的光学斩波轮每机械旋转 360°，将前进 n×360°opt（光学角度）。我们将这些单位指定为光学度数 (°opt) 和机械度数 (°mech)。图 2 显示了 6 槽叶片的区别。

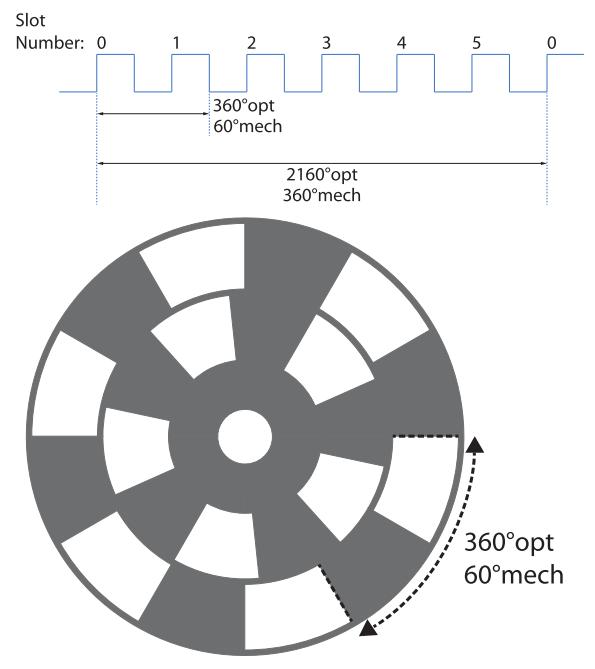
图2：6槽斩波器叶片的光学相位和机械相位之间的关系。

  以机械角度表示抖动可以使测量结果看起来更有利 n 倍。例如，1°mech 的抖动对于 6 槽叶片来说是 6°opt，对于 100 槽叶片来说是 100°opt。然而，光学斩波器用户对叶片的机械方向不太感兴趣，因为理想情况下，所有 n 个槽都是相同的。换句话说，旋转机械斩波器只是用于调制光源的许多方法中的一种，并且抖动规格及其单位应该与该方法无关。

抖动的来源：

机械斩波器的光学抖动有多种因素，定义和讨论如下。

电动机中确定性扭矩的一个特别明显的来源被称为齿槽扭矩，该术语旨在唤起诸如滴答作响的时钟之类的有齿装置的离散旋转步骤。齿槽转矩取决于转子的角取向，即转子轴，并且将以随着每次机械旋转而重复的模式来调节轴速度。对于直流电动机，齿槽效应是由于转子和定子之间的磁力变化而产生的。齿槽效应在直流步进电机中非常明显，在典型的开槽无刷直流电机中也存在。

  相比之下，SR542 中使用的无槽无刷直流电机旨在最大限度地减少转子-定子相互作用力的变化，从而提供均匀的旋转扭矩。然而，完全消除齿槽效应具有挑战性，特别是在低速情况下。在较高速度下，转子的惯性往往会平滑由任何齿槽扭矩引起的加速度。

测量和结果：

为了评估上述每种效应对斩波器抖动的影响，我们收集了 N 个周期的光信号，并将测量的周期绘制为时间的函数，以及所有测量值的直方图。 我们不是以周期为单位绘制（秒），我们是以光学相位（°opt）为单位进行绘制。每个测量周期 Ti 均转换为相位误差 δψi，如下所示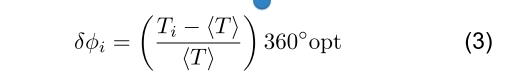

其中，T是所有N次测量的平均周期。

相位抖动只是 N 个相位误差测量的 RMS 值，并可视化为相位误差直方图的宽度。

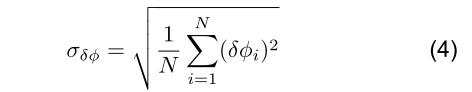
图 3 为设定点斩波频率为 1 Hz 的 5 槽叶片的周期误差与时间的关系示例。原始周期测量与时间的关系如图 3a 所示。在图 3b 中，所有测量的周期误差都被收集到直方图中。所有周期测量值的直方图分布宽度（蓝色轮廓），以平均值的标准差 (σ) 为特征，为 0.359°opt。该分布包括上面讨论的所有抖动源，并代表以 1 Hz 运行的典型斩波实验会经历的抖动。

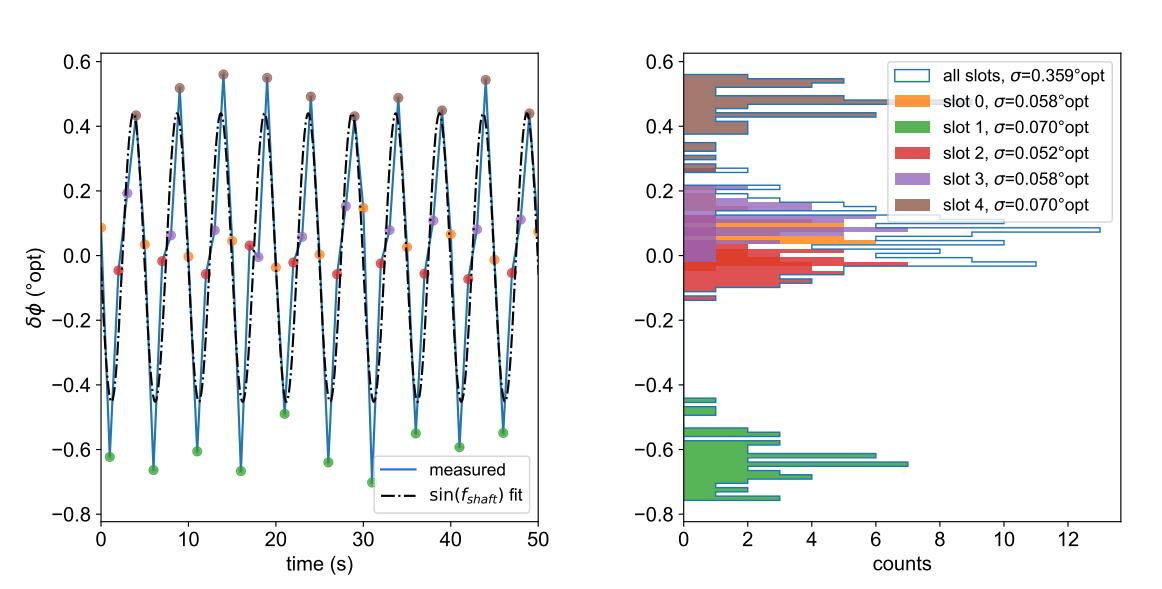
(图3a左侧)周期误差与时间。数据点根据其槽号进行颜色编码（即每5个数据点为相同颜色）。对数据进行正弦拟合，频率等于轴频率（fchop/5），作为眼睛的引导，以突出对相位误差的确定性贡献。仅显示采集数据的前10次机械旋转。

(图3b右侧)来自图3a的直方图数据。颜色编码与来自图3a的颜色编码匹配。计算“所有槽”和单个槽的σ值，并将其报告为与平均相位误差的RMS偏差。

对于 n 槽叶片，每第 n 个周期测量都是对同一槽的重复测量。因此，我们为与该叶片的 5 个槽相对应的周期测量值分配不同的颜色。以槽 1 为例（绿色）。它的平均周期误差约为−0.65°opt。这意味着标记槽位 1 周期结束的边缘比预期早 0.65°opt。非确定性抖动将绿色分布的宽度设置为仅为 0.070°opt，因此相位误差从一转到另一转的再现性非常好，并且由确定性误差主导。简单地说，对于单个槽位，相位误差的确定性源确定平均值，而非确定性源确定抖动（标准偏差）。  

在图 3a 中，提供了 f轴 处的正弦曲线拟合，以突出 5 槽叶片在这种低斩波频率下的大部分“全槽” 光学抖动可归因于相位误差的确定性来源。从数量上看，“全槽”抖动比“单槽位”平均值大近六倍。然而，归根结底，典型的斩波器实验对所有抖动贡献的总和很敏感，重要的指标是“全槽”抖动。只有当用户可以将光学快门布置成每第n个光学周期通过一次时，他们才能利用由“单槽位”相位误差分布 所示的优异可重复性。  

请注意，确定性并不一定意味着正弦曲线。虽然安装同心度会带来与 Φ 轴呈正弦曲线的周期误差，但叶片缺陷会引入槽与槽之间的随机周期误差（每次机械旋转都会重复，但不一定是正弦曲线）。根据经验，我们发现齿槽误差通常以 ∼sin( Φ轴) 或 ∼sin(2 Φ轴) 形式出现，但这取决于斩波电机的结构。

接下来让我们看看相位误差测量值随斩波频率的变化。同心度和叶片缺陷将导致与频率无关的相位误差，因为它们只取决于几何形状。然而，齿槽误差将在更高的速度下减小，因为位置相关的齿槽加速度将具有更少的时间来改变旋转轴的速度。因此，通过考虑周期误差测量的频率依赖性，可以对确定性贡献进行一些分离。

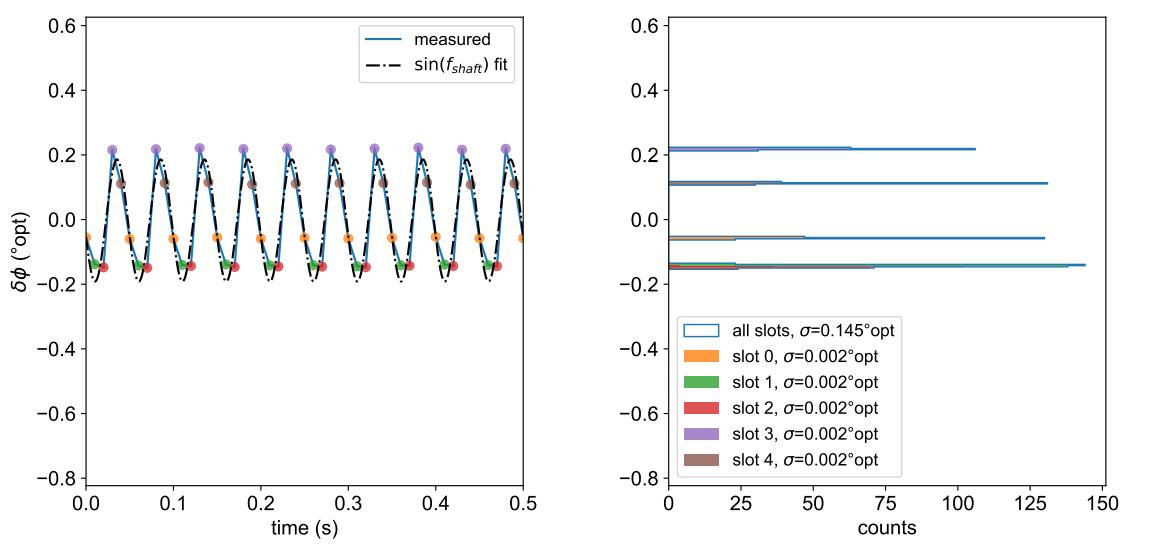
(图4a) 相位误差与时间的关系。          (图4b) 相位误差直方图。

图 4：fchop = 100 Hz 时 SR542 5 槽叶片的相位误差测量。

图 4 显示了相同的 5 槽斩波叶片，其运行速度提高了 100 倍，其中 fchop = 100 Hz。与图 3 相比（为了便于比较，保留了 y 轴比例），很容易看出在较高轴速度下增加角动量的有益效果：f轴 处正弦调制的总体幅度减小，并且每个槽的“单槽”变化大大减少。在此速度下，转子的惯性“平滑”了齿槽扭矩，剩余的正弦相位误差可能是由于叶片安装位置的较小同心度误差造成的。 同时，在直方图（图 4b） 中看到窄峰表明出色的电机速度控制。

请注意，槽 1 和 2（绿色和红色）彼此重叠，因此仅分辨了 4 个峰。此外，没有方法可以保证每次试验中的槽位都是相同的，因此图 4 中的槽位 0 不一定与图 3 中的槽位相同。

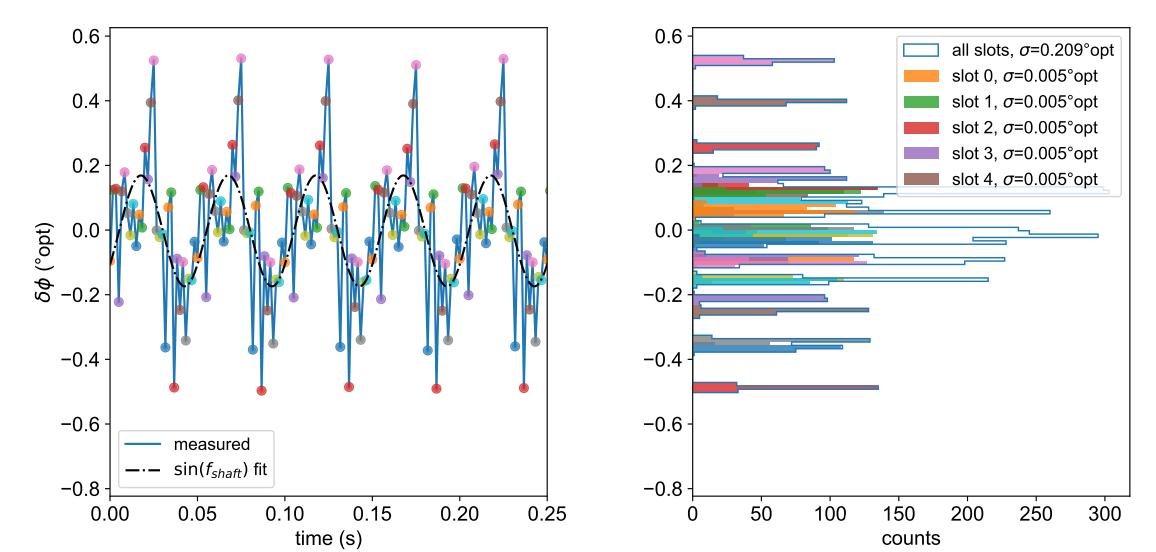
(图5a) 相位误差与时间的关系。    (图5a) 相位误差与时间的关系。

图 5：fchop = 600 Hz 时 SR542 30 槽叶片的相位误差测量。

图 5 显示了 30 槽频率为600Hz的相位误差和抖动，在与图 4 相同的轴速度 f轴 = 20 Hz 下获得，齿槽效应被很大程度上抑制，并且周期的正弦变化可能是由于同心度误差造成的（注意与图 4 类似的正弦幅度）。然而，相位误差模式不再主要是正弦曲线。我们继续提供正弦拟合，因为（1）它有助于识别同心度误差，（2）它可以作为 Φshaft 的参考，强调相位误差相对于轴方向的重复性。

正弦残差（减去正弦拟合后剩余的相位误差）包含来自叶片缺陷（在某种程度上，这些缺陷是随机的而不是正弦本身）和将高斯噪声与该指纹卷积的随机误差的确定性贡献。颜色编码使得很容易看到相位误差图案（“指纹”），其随着每次机械旋转而高度重复。

抖动与频率：

5 槽、10 槽、30 槽和 100 槽斩波叶片的抖动数据与斩波频率的函数关系如图 6 所示。圆圈表示“所有槽”RMS 抖动，而三角形表示平均值。每个斩波频率处的 n 个“单槽”抖动值。这些图中还显示了每个斩波器叶片的已发布抖动规格（虚线）。

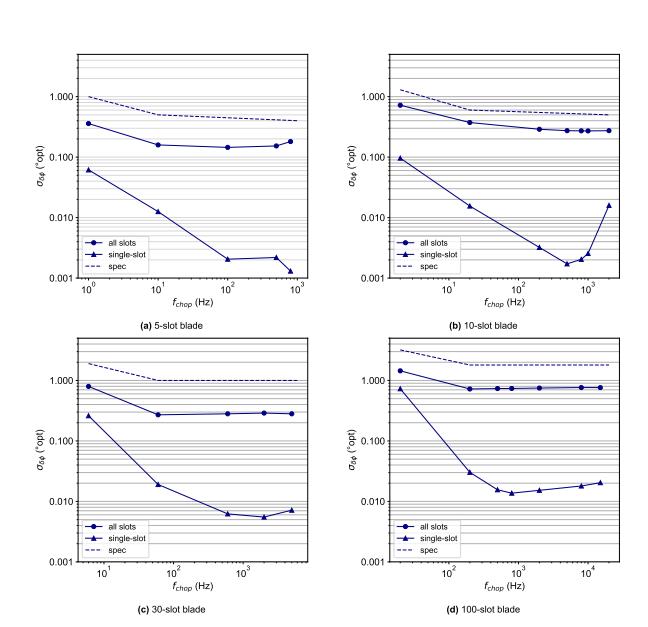
图6：RMS相位误差与频率的关系。

抖动与叶片和频率相关，但这些图中确实出现了一些总体趋势。在低速下，小力（随机的和确定性的，即齿槽效应）会对相位误差产生很大的影响，这一点在最低斩波速率下“所有槽”和“单槽”指标观察到的抖动增加中显而易见。 SR542 斩波器头的工厂校准包括齿槽加速度的测量。这些测量结果用于计算 SR542 控制器用于消除齿槽转矩的补偿电流。因此，我们能够将斩波器的工作范围扩展到比上一代斩波器慢一个数量级的轴速度。除了最低的轴速度之外，“全槽”抖动通常会接近某个渐近值，即由叶片缺陷和同心度误差的频率无关贡献设定的本底噪声，而“单槽”抖动继续由于惯性平滑而改善。

表1中列出了实测性能和已发布规格的表格比较。为简单起见，为每个叶片选择单个斩波频率。显示了“所有槽”和“单槽”抖动值，但由于“所有槽”测量与大多数斩波实验相关，因此应将该值与已发布的规格进行比较。

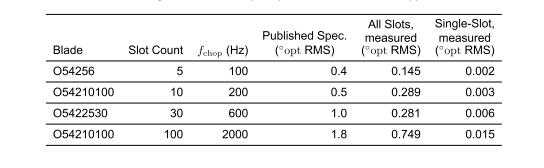
表1：各种斩波器叶片在选定斩波频率下的相位抖动。

结论：

 最后，在比较不同光斩波器的抖动规格时，请注意单位。光学度数的使用是最相关和透明的。此外，应该使用所考虑的叶片的所有槽来计算抖动统计数据。

这里提出的分析使用相位误差测量与时间的关系以及相应的直方图，对于隔离各种抖动源具有指导意义，特别是在多个频率设定点重复时。这种分析有助于了解机械斩波器的优点和局限性，为实验操作参数的选择提供信息，或诊断大于预期的相位噪声。

有几个来源会影响斩波光束上的整体抖动。可以是随机的或确定性的，并且随着机械旋转而重复，如齿槽扭矩、叶片缺陷和叶片的非同心安装等情况。一些确定性来源（齿槽效应和同心度）将与 Φ轴（或其谐波）大致呈正弦关系，而其他来源（叶片缺陷）可以作为轴方向的函数随机分散。通常，以可用的最高轴速度进行斩波有利于消除齿槽扭矩引起的误差。同时，叶片缺陷和同心度会产生与频率无关的误差。为了最大限度地减少同心度误差，在将叶片安装到轮毂上时应注意不要引入径向偏移。最后，由于叶片制造误差通常具有固定的横向尺寸，因此这些误差将对较高槽数的叶片产生更显着的影响，因此使用尽可能少的槽数也是有利的。

参考文献

[1] Dana F. Geiger. Phaselock Loops for DC Motor Speed Control. John Wiley & Sons, 1981.